It is known that the language of all encoded permutations of a TPN is rational, and thus is it indeed possible to turn a TPN into an automaton. The idea is to inspect all dispositions of tokens within the TPN and find equivalence classes of these dispositions, for more details consult [3]. Adding a constraint, which limits the number of tokens at any time within the TPN, is also considered in this chapter.
The algorithms featured in this chapter do not return the minimal automata representing the input TPN as they are exactly visualising the equivalence classes of the dispositions of the tokens in the TPN. The automaton can be minimalised by choice, as it simplifies future computations involving the automaton also is makes the automata more legible.
‣ GraphToAut( g, innode, outnode ) | ( function ) |
Returns: An automaton representing the input TPN.
GraphToAut turns an array represented directed graph, with a distinct input node and a distinct output node, into the corresponding automaton, that accepts the language build by the resulting rank encoded permutations of the directed graph.
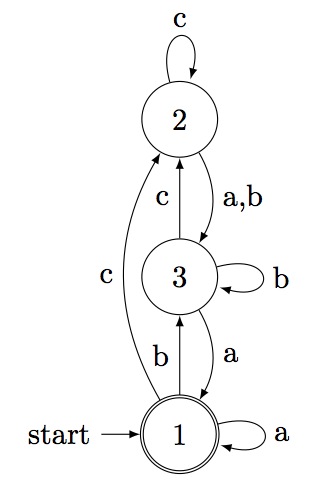
gap> x:=Seqstacks(2,2); [ [ 2 ], [ 3, 4 ], [ 2 ], [ 5, 6 ], [ 4 ], [ ] ] gap> aut:=GraphToAut(x,1,6); < epsilon automaton on 4 letters with 64 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 3 letters with 3 states > gap> Display(aut); | 1 2 3 -------------- a | 1 3 1 b | 3 3 3 c | 2 2 2 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The minimal automaton corresponding to Seqstacks(2,2) is:

gap> x:=Parstacks(2,2); [ [ 2, 4 ], [ 3, 6 ], [ 2 ], [ 5, 6 ], [ 4 ], [ ] ] gap> aut:=GraphToAut(x,1,6); < epsilon automaton on 5 letters with 66 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 4 letters with 9 states > gap> Display(aut); | 1 2 3 4 5 6 7 8 9 -------------------------------- a | 1 2 1 3 2 2 6 6 3 b | 3 2 3 3 4 3 6 9 3 c | 9 2 9 4 6 6 4 9 9 d | 8 2 8 7 5 5 7 8 8 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The rank encoded permutations of Parstacks(2,2) are accepted by the following automaton:
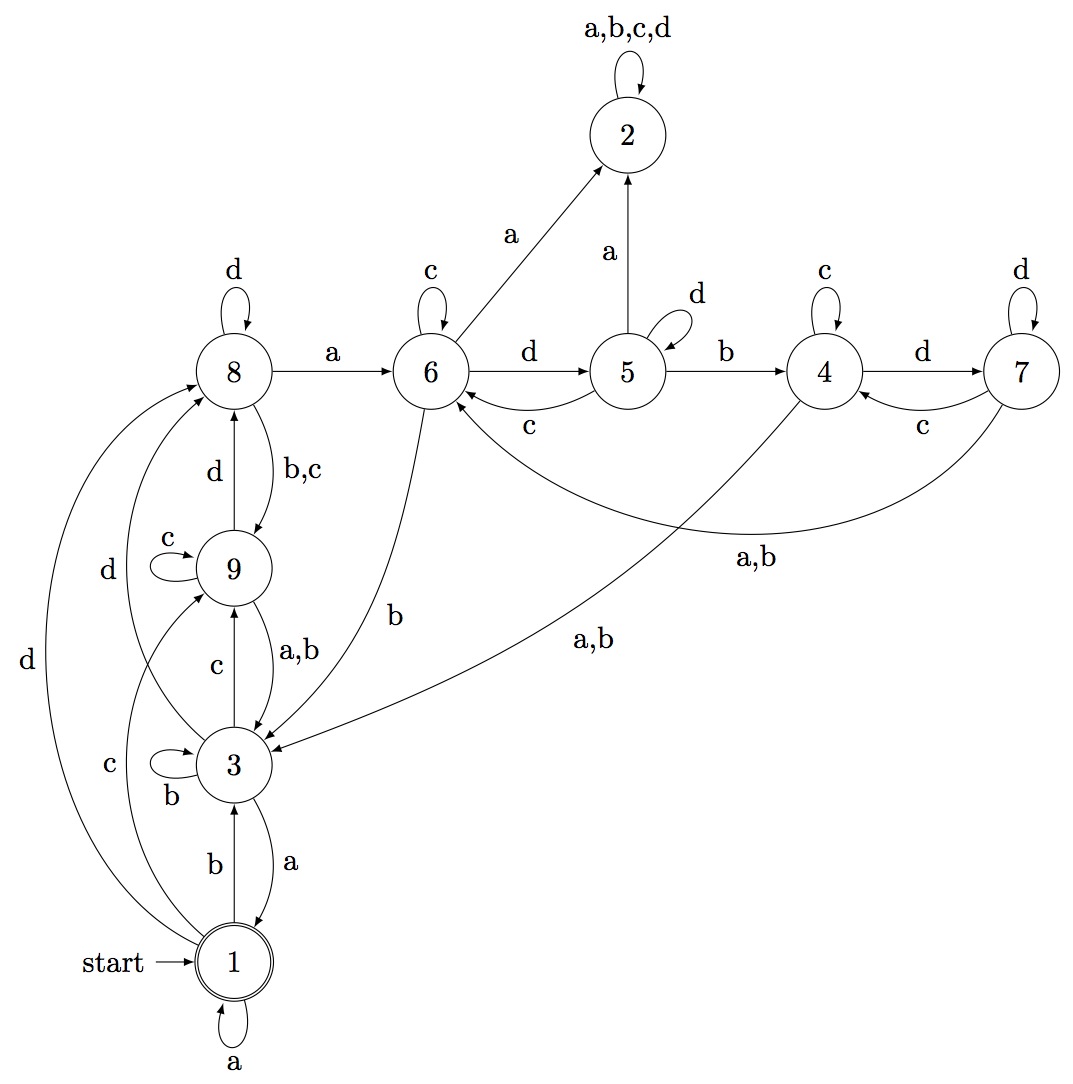
gap> x:=BufferAndStack(3,2); [ [ 2 .. 4 ], [ 5 ], [ 5 ], [ 5 ], [ 6, 7 ], [ 5 ], [ ] ] gap> aut:=GraphToAut(x,1,7); < epsilon automaton on 5 letters with 460 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 4 letters with 4 states > gap> Display(aut); | 1 2 3 4 ----------------- a | 1 4 1 3 b | 3 4 3 3 c | 4 4 4 4 d | 2 2 2 2 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The following automaton represents the language of rank encoded permutations that are output by BufferAndStack(3,2):
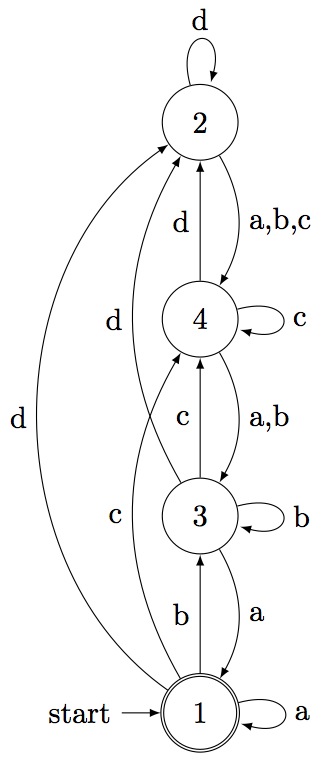
gap> x:=[[2,3],[4],[5],[3,6],[6],[]]; [ [ 2, 3 ], [ 4 ], [ 5 ], [ 3, 6 ], [ 6 ], [ ] ] gap> aut:=GraphToAut(x,1,6); < epsilon automaton on 4 letters with 80 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 3 letters with 8 states > gap> Display(aut); | 1 2 3 4 5 6 7 8 ----------------------------- a | 1 3 1 4 6 1 6 1 b | 3 8 3 4 4 6 6 6 c | 2 2 2 4 5 5 7 7 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The input TPN here is the first network described in Chapter 2.. The language of rank encoded permutations of this token passing network is accepted by the following automaton:
‣ ConstrainedGraphToAut( g, innode, outnode, capacity ) | ( function ) |
Returns: An automaton representing the input TPN with bounded capacity.
ConstrainedGraphToAut builds an epsilon automaton based on the same idea as GraphToAut, so it takes a list representation of a directed graph, a designated input node and a distinct output node, but additionally there is the constraint that there can be at most capacity tokens in the graph, at any time.
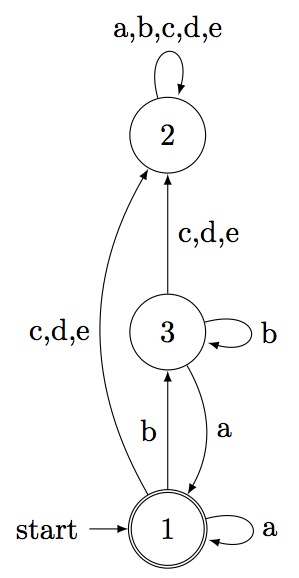
gap> x:=Seqstacks(2,2); [ [ 2 ], [ 3, 4 ], [ 2 ], [ 5, 6 ], [ 4 ], [ ] ] gap> aut:=ConstrainedGraphToAut(x,1,6,2); < epsilon automaton on 6 letters with 21 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 5 letters with 3 states > gap> Display(aut); | 1 2 3 -------------- a | 1 2 1 b | 3 2 3 c | 2 2 2 d | 2 2 2 e | 2 2 2 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The rank encoded permutations of Seqstacks(2,2), where at any time there are at most 2 tokens within the network, are accepted by the following automaton:
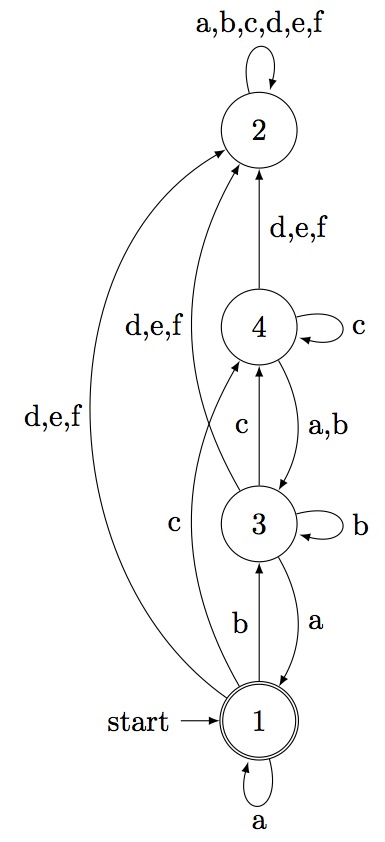
gap> x:=BufferAndStack(3,2); [ [ 2 .. 4 ], [ 5 ], [ 5 ], [ 5 ], [ 6, 7 ], [ 5 ], [ ] ] gap> aut:=ConstrainedGraphToAut(x,1,6,3); < epsilon automaton on 7 letters with 112 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 6 letters with 4 states > gap> Display(aut); | 1 2 3 4 ----------------- a | 1 2 1 3 b | 3 2 3 3 c | 4 2 4 4 d | 2 2 2 2 e | 2 2 2 2 f | 2 2 2 2 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The automaton corresponding to BufferAndStack(3,2) with limited capacity of 3 tokens is:
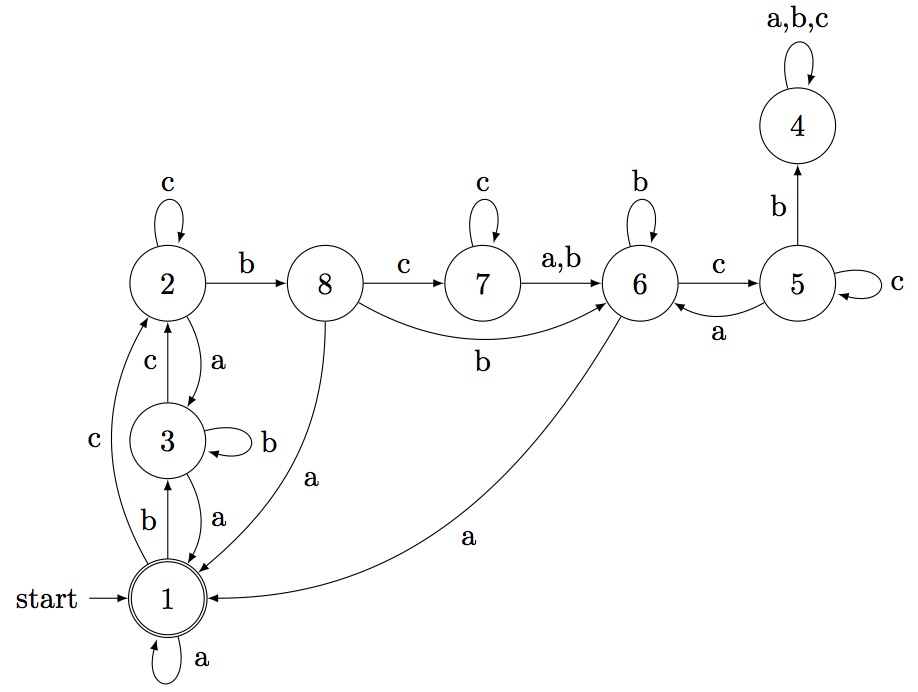
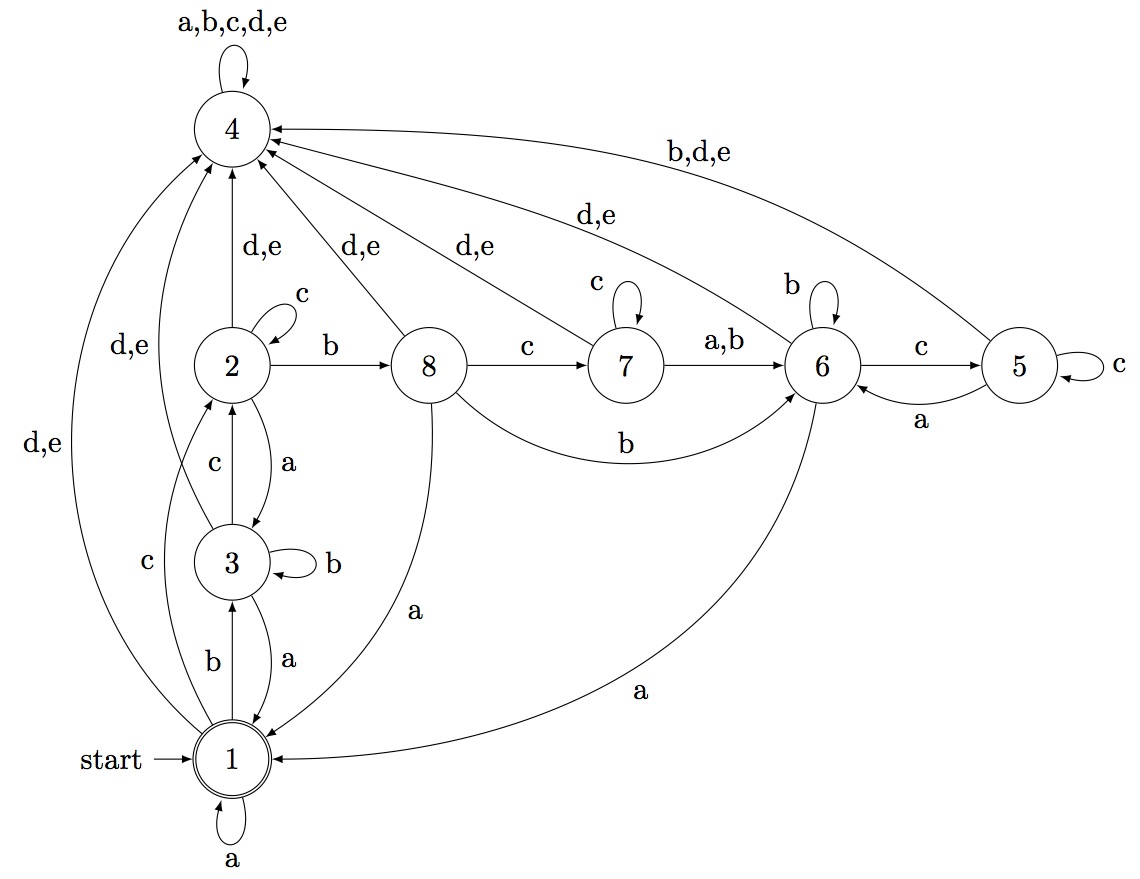
gap> x:=[[2,3],[4],[5],[3,6],[6],[]]; [ [ 2, 3 ], [ 4 ], [ 5 ], [ 3, 6 ], [ 6 ], [ ] ] gap> aut:=ConstrainedGraphToAut(x,1,6,3); < epsilon automaton on 6 letters with 48 states > gap> aut:=MinimalAutomaton(aut); < deterministic automaton on 5 letters with 8 states > gap> Display(aut); | 1 2 3 4 5 6 7 8 ----------------------------- a | 1 3 1 4 6 1 6 1 b | 3 8 3 4 4 6 6 6 c | 2 2 2 4 5 5 7 7 d | 4 4 4 4 4 4 4 4 e | 4 4 4 4 4 4 4 4 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
The automaton that accepts the language of rank encoded permutations of the token passing network, from Chapter 2., with at most 3 tokens in the network at anytime, is:
generated by GAPDoc2HTML