Permutation pattern classes can be determined using their corresponding basis. The basis of a pattern class is the anti-chain of the class, under the order of containment. A permutation \(\pi\) contains another permutation \(\sigma\) (of shorter length) if there is a subsequence in \(\pi\), which is isomorphic to \(\sigma\).
With the rational language of the rank encoded class, it is also possible to find the rational language of the basis and vice versa. Several specific kinds of transducers are used in this process. [2]
‣ Transducer( states, init, transitions, accepting ) | ( function ) |
Returns: A record that represents a transducer.
A transducer is essentially an automaton, where running through the process does not determine whether the input is accepted, but the input is translated to another language, over a different alphabet.
Formally a transducer is a six-tuple with: \(Q\) being the set of states, \(S\) the input alphabet, \(G\) the output alphabet, \(I \in Q\) the start state, \(A \subseteq Q\) the set of accept states, and with the transition function \(f: Q \times (S \cup \{e\}) \rightarrow Q \times (G \cup \{e\})\), where \(e\) is the empty word.
In this function the transducer is stored by defining how many states there are, which one (by index) is the start or initial state, the transitions are of the form [inputletter,outputletter,fromstate,tostate] and a list of accept states. The input and output alphabet are determined by the input and output letters on the transitions.
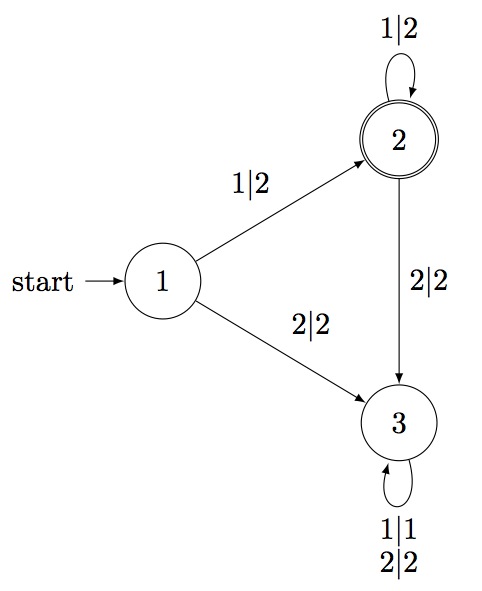
gap> trans:=Transducer(3,1,[[1,2,1,2],[1,2,2,2],[2,2,1,3],[2,2,2,3], > [1,1,3,3],[2,2,3,3]],[2]); rec( accepting := [ 2 ], initial := 1, states := 3, transitions := [ [ 1, 2, 1, 2 ], [ 1, 2, 2, 2 ], [ 2, 2, 1, 3 ], [ 2, 2, 2, 3 ], [ 1, 1, 3, 3 ], [ 2, 2, 3, 3 ] ] ) gap>
This transducer can be visualised as the following graph:

‣ DeletionTransducer( k ) | ( function ) |
Returns: A transducer over k+1 states.
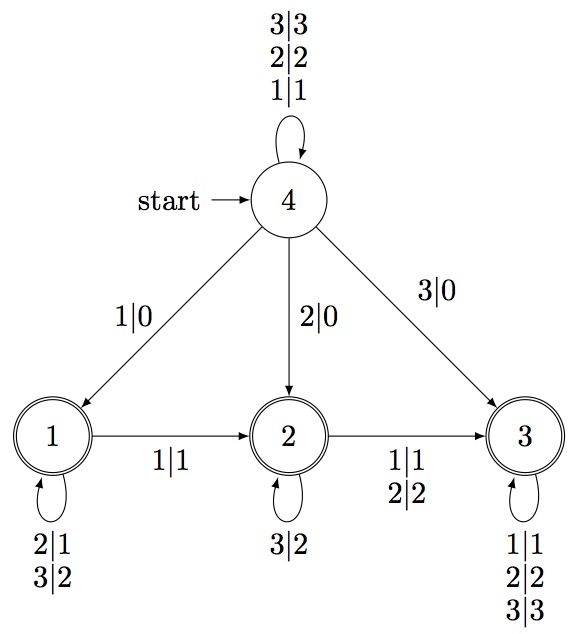
A deletion transducer is a transducer that deletes one letter of a rank encoded permutation and returns the correct rank encoding of the new permutation. The deletion transducer over k deletes letters over the set of all rank encoded permutations with highest rank k. Specifically, running through a deletion transducer with a rank encoded permutation, of highest rank k, will lead to the set of all rank encoded permutations that have one letter of the initial permutation removed. It is important to note that computing these shorter permutations with the transducer, is done by reading the input permutation from right to left. For example the deletion transducer with k=3, looks as follows:
gap> DeletionTransducer(3); rec( accepting := [ 1 .. 3 ], initial := 4, states := 4, transitions := [ [ 1, 1, 4, 4 ], [ 1, 0, 4, 1 ], [ 2, 1, 1, 1 ], [ 1, 1, 1, 2 ], [ 3, 2, 1, 1 ], [ 1, 1, 2, 3 ], [ 1, 1, 3, 3 ], [ 2, 2, 4, 4 ], [ 2, 0, 4, 2 ], [ 3, 2, 2, 2 ], [ 2, 2, 2, 3 ], [ 2, 2, 3, 3 ], [ 3, 3, 4, 4 ], [ 3, 0, 4, 3 ], [ 3, 3, 3, 3 ] ] ) gap>
‣ TransposedTransducer( t ) | ( function ) |
Returns: A new transducer with interchanged input and output letters on each transition.
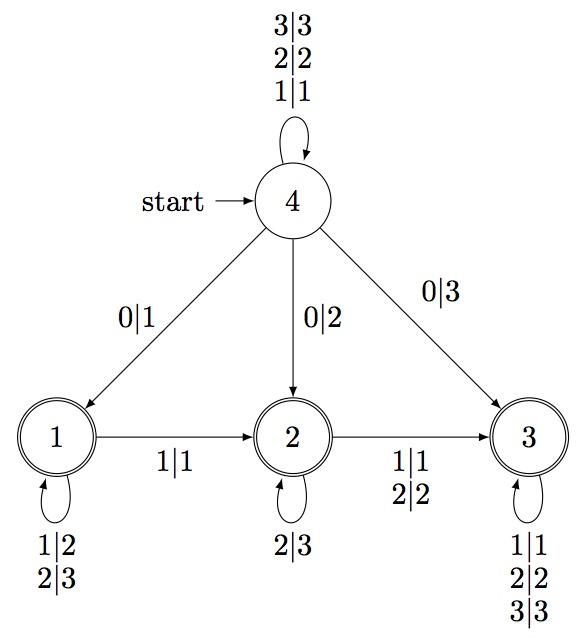
A transducer is transposed when all origins and destinations of transitions are left the same as before but the input and output letters on each transition are interchanged. Taking the deletion transducer from above, its transpose looks as follows:
gap> TransposedTransducer(DeletionTransducer(3)); rec( accepting := [ 1 .. 3 ], initial := 4, states := 4, transitions := [ [ 1, 1, 4, 4 ], [ 0, 1, 4, 1 ], [ 1, 2, 1, 1 ], [ 1, 1, 1, 2 ], [ 2, 3, 1, 1 ], [ 1, 1, 2, 3 ], [ 1, 1, 3, 3 ], [ 2, 2, 4, 4 ], [ 0, 2, 4, 2 ], [ 2, 3, 2, 2 ], [ 2, 2, 2, 3 ], [ 2, 2, 3, 3 ], [ 3, 3, 4, 4 ], [ 0, 3, 4, 3 ], [ 3, 3, 3, 3 ] ] ) gap>
‣ InvolvementTransducer( k ) | ( function ) |
Returns: A transducer over k+1 states, with a k sized alphabet.
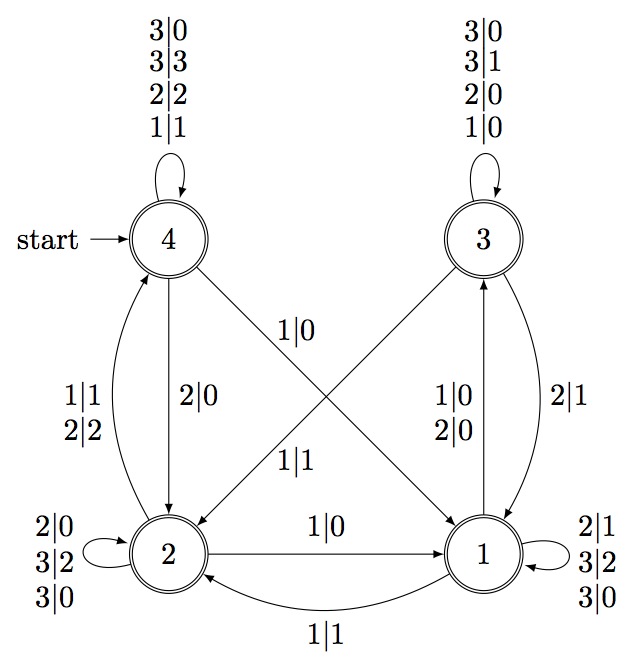
An involvement transducer is a transducer over k+1 states, and deletes any number of letters in a rank encoded permutation, of rank at most k.
gap> InvolvementTransducer(3); rec( accepting := [ 1 .. 4 ], initial := 4, states := 4, transitions := [ [ 1, 1, 1, 2 ], [ 1, 0, 1, 3 ], [ 2, 1, 1, 1 ], [ 2, 0, 1, 3 ], [ 3, 2, 1, 1 ], [ 3, 0, 1, 1 ], [ 1, 1, 2, 4 ], [ 1, 0, 2, 1 ], [ 2, 2, 2, 4 ], [ 2, 0, 2, 2 ], [ 3, 2, 2, 2 ], [ 3, 0, 2, 2 ], [ 1, 1, 3, 2 ], [ 1, 0, 3, 3 ], [ 2, 1, 3, 1 ], [ 2, 0, 3, 3 ], [ 3, 1, 3, 3 ], [ 3, 0, 3, 3 ], [ 1, 1, 4, 4 ], [ 1, 0, 4, 1 ], [ 2, 2, 4, 4 ], [ 2, 0, 4, 2 ], [ 3, 3, 4, 4 ], [ 3, 0, 4, 4 ] ] ) gap>
‣ CombineAutTransducer( aut, trans ) | ( function ) |
Returns: An automaton consisting of a combination of aut and trans.
Combining automata and transducers is done over the natural "translation" of the by the automaton accepted language through the transducer and then building a new automaton that accepts the new language. The function CombineAutTransducer does this process and returns the new non-deterministic automaton.
gap> a:=Automaton("det",1,1,[[1]],[1],[1]); < deterministic automaton on 1 letters with 1 states > gap> AutToRatExp(a); a* gap> t:=Transducer(2,1,[[1,2,1,2],[2,1,1,2], > [1,1,2,1],[2,2,2,1]],[1]); rec( accepting := [ 1 ], initial := 1, states := 2, transitions := [ [ 1, 2, 1, 2 ], [ 2, 1, 1, 2 ], [ 1, 1, 2, 1 ], [ 2, 2, 2, 1 ] ] ) gap> res:=CombineAutTransducer(a,t); < non deterministic automaton on 2 letters with 2 states > gap> AutToRatExp(res); (ba)* gap> Display(res); | 1 2 ------------------- a | [ 1 ] b | [ 2 ] Initial state: [ 1 ] Accepting state: [ 1 ] gap>
‣ BasisAutomaton( a ) | ( function ) |
Returns: An automaton that accepts the rank encoded permutations of the basis of the input automaton a.
Every pattern class has a basis that consists of the smallest set of permutations which do not belong to the class. Using
\[B(L)=(L^{r} D^{t})^{r} \cap L^{c}\]
it is possible using the deletion transducer \(D\) and the language of rank encoded permutations \(L\) to find the language of the rank encoded permutations of the basis \(B(L)\), and thus the basis.
gap> x:=Parstacks(2,2); [ [ 2, 4 ], [ 3, 6 ], [ 2 ], [ 5, 6 ], [ 4 ], [ ] ] gap> xa:=GraphToAut(x,1,6); < epsilon automaton on 5 letters with 66 states > gap> ma:=MinimalAutomaton(xa); < deterministic automaton on 4 letters with 9 states > gap> Display(ma); | 1 2 3 4 5 6 7 8 9 -------------------------------- a | 1 2 1 3 2 2 6 6 3 b | 3 2 3 3 4 3 6 9 3 c | 9 2 9 4 6 6 4 9 9 d | 8 2 8 7 5 5 7 8 8 Initial state: [ 1 ] Accepting state: [ 1 ] gap> ba:=BasisAutomaton(ma); < deterministic automaton on 4 letters with 9 states > gap> Display(ba); | 1 2 3 4 5 6 7 8 9 -------------------------------- a | 2 2 1 3 4 2 2 2 2 b | 2 2 2 2 2 4 1 2 8 c | 2 2 2 2 2 2 1 2 2 d | 2 2 2 9 2 2 5 6 2 Initial state: [ 7 ] Accepting states: [ 1, 5 ] gap> AutToRatExp(ba); d(a(dbdb)*aaU@)UbUc gap>
Ignoring the trailing UbUc which essentially are noise, the basis of the pattern class indicates which permutations are avoided in this particular class. The shortest permutation in the basis, looking at the rational expression, is \(daaa\), which can be translated to 4111 and decoded to the permutation 4123.
‣ ClassAutomaton( a ) | ( function ) |
Returns: The automaton that accepts permutations of the class in their rank encoding.
The function ClassAutomaton does the reverse process of BasisAutomaton. Namely it takes the automaton that represents the language of the rank encoded basis of a permutation class, and using the formula
\[L=B_{k} \cap ((B(L)^{r} I^{t})^{c} )^{r}\]
returns the automaton that accepts the rank encoded permutations of the class. In the formula, \(B_{k}\) is the automaton that accepts all permutations of any length with highest rank \(k\), \(B(L)\) is the automaton that represents the basis and \(I\) is the involement transducer.
gap> xa:=Automaton("det",9,4,[[2,2,1,3,4,2,2,2,2],[2,2,2,2,2,4,1,2,8], > [2,2,2,2,2,2,1,2,2],[2,2,2,9,2,2,5,6,2]],[7],[1,5]); < deterministic automaton on 4 letters with 9 states > gap> ca:=ClassAutomaton(xa); < deterministic automaton on 4 letters with 9 states > gap> Display(ca); | 1 2 3 4 5 6 7 8 9 -------------------------------- a | 1 2 1 3 2 2 6 6 3 b | 3 2 3 3 4 3 6 9 3 c | 9 2 9 4 6 6 4 9 9 d | 8 2 8 7 5 5 7 8 8 Initial state: [ 1 ] Accepting state: [ 1 ] gap> IsPossibleGraphAut(ca); true gap>
‣ BoundedClassAutomaton( k ) | ( function ) |
Returns: An automaton that accepts all rank encoded permutations, with highest rank being k.
The bounded class automaton, is an automaton that accepts all rank encoded permutations, of any length, with highest rank k.
gap> BoundedClassAutomaton(3); < deterministic automaton on 3 letters with 3 states > gap> Display(last); | 1 2 3 -------------- a | 1 1 2 b | 2 2 2 c | 3 3 3 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
‣ ClassAutFromBaseEncoding( base, k ) | ( function ) |
Returns: The class automaton from a list of rank encoded basis permutations.
Given the permutations in the basis, in their rank encoded form, and the bound of the rank of the permutations of the class, ClassAutFromBaseEncoding builds the automaton that accepts rank encoded permutations of the class.
gap> ClassAutFromBaseEncoding([[4,1,1,1]],4); < deterministic automaton on 4 letters with 7 states > gap> Display(last); | 1 2 3 4 5 6 7 -------------------------- a | 1 2 1 3 2 2 6 b | 3 2 3 3 4 3 4 c | 4 2 4 4 6 6 4 d | 7 2 7 7 5 5 7 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
‣ ClassAutFromBase( perms, k ) | ( function ) |
Returns: The class automaton from a list of permutations of the basis.
Taking perms which is the list of permutations in the basis and k an integer which indicates the highest rank in the encoded permutations of the class, ClassAutFromBase constructs the automaton that accepts the language of rank encoded permutations of the class.
gap> ClassAutFromBase([[4,1,2,3]],4); < deterministic automaton on 4 letters with 7 states > gap> Display(last); | 1 2 3 4 5 6 7 -------------------------- a | 1 2 1 3 2 2 6 b | 3 2 3 3 4 3 4 c | 4 2 4 4 6 6 4 d | 7 2 7 7 5 5 7 Initial state: [ 1 ] Accepting state: [ 1 ] gap>
‣ ExpandAlphabet( a, newAlphabet ) | ( function ) |
Returns: The automaton a, over the alphabet of size newAlphabet.
Given an automaton and the size of the new alphabet, which has to be bigger than the size of the alphabet in a , ExpandAlphabet changes the automaton a to contain an alphabet of size newAlphabet. The new letters have no transitions within the automaton.
gap> aut:=Automaton("det",3,2,[[2,2,3],[3,3,3]],[1],[3]); < deterministic automaton on 2 letters with 3 states > gap> Display(aut); | 1 2 3 -------------- a | 2 2 3 b | 3 3 3 Initial state: [ 1 ] Accepting state: [ 3 ] gap> ExpandAlphabet(aut,4); < deterministic automaton on 4 letters with 3 states > gap> Display(last); | 1 2 3 -------------- a | 2 2 3 b | 3 3 3 c | d | Initial state: [ 1 ] Accepting state: [ 3 ] gap>
It is obvious that the direct sum of two rational pattern classes is also rational. But the skew sum of two rational pattern classes does not imply that the resulting pattern class is rational, because if the second class in the sum has infinitely many permutations, the alphabet of the skew sum class will be infinite and thusly the resulting class will not be rational.
‣ ClassDirectSum( aut1, aut2 ) | ( function ) |
Returns: An automaton that corresponds to the direct sum of aut1 with aut2.
ClassDirectSum builds the concatenation automaton of aut1 with aut2, which corresponds to the pattern class aut1 \(\oplus\) aut2.
gap> a:=BasisAutomaton(GraphToAut(Parstacks(2,2),1,6)); < deterministic automaton on 4 letters with 9 states > gap> AutToRatExp(a); d(a(dbdb)*aaU@)UbUc gap> b:=MinimalAutomaton(GraphToAut(Seqstacks(2,2),1,6)); < deterministic automaton on 3 letters with 3 states > gap> AutToRatExp(b); ((cc*(aUb)Ub)(cc*(aUb)Ub)*aUa)* gap> ab:=ClassDirectSum(a,b); < deterministic automaton on 4 letters with 11 states > gap> AutToRatExp(ab); ((d(acUc)c*(aUb)Ud(abUb))(cc*(aUb)Ub)*aUda(d(bdbd)*bdbaaUa)UbUc)((cc*(aUb)U\ b)(cc*(aUb)Ub)*aUa)*Ud(aU@) gap>
It is of interest to see what permutations and how many of different length are accepted by the class, respectively the basis.
In this section, the examples will be inspecting the basis automaton of the token passing network containing 2 stacks of capacity 2, which are situated in parallel to each other.
gap> x:=Parstacks(2,2); [ [ 2, 4 ], [ 3, 6 ], [ 2 ], [ 5, 6 ], [ 4 ], [ ] ] gap> xa:=GraphToAut(x,1,6); < epsilon automaton on 5 letters with 66 states > gap> ma:=MinimalAutomaton(xa); < deterministic automaton on 4 letters with 9 states > gap> ba:=BasisAutomaton(ma); < deterministic automaton on 4 letters with 9 states > gap> AutToRatExp(ba); d(a(dbdb)*aaU@)UbUc gap>
‣ Spectrum( aut[, int] ) | ( function ) |
Returns: A list indicating how many words of each length from 1 to int or 15 (default) are accepted by the automaton.
Each entry in the returned list indicates how many words of length the index of the entry are accepted by the automaton aut. The length of the list is by default 15, but if this is too much or too little the second optional argument regulates the length of the list.
gap> Spectrum(ba); [ 3, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0 ] gap> Spectrum(ba,20); [ 3, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1 ] gap>
‣ NumberAcceptedWords( aut, len ) | ( function ) |
Returns: The number of words of length len accepted by the automaton aut.
Given the automaton aut and the integer len, NumberAcceptedWords determines how many words of length len are accepted by the automaton.
gap> NumberAcceptedWords(ba,1); 3 gap> NumberAcceptedWords(ba,16); 1 gap>
‣ AutStateTransitionMatrix( aut ) | ( function ) |
Returns: A matrix containing the number of transitions between states of the automaton aut.
In the matrix computed by AutStateTransitionMatrix the rows are indexed by the state the transitions are originating from, the columnns are indexed by the states the transitions are ending at. Each entry \(a_{i,j}\) of the matrix represents the number of transitions from the state \(i\) to the state \(j\).
gap> AutStateTransitionMatrix(ba); [ [ 0, 4, 0, 0, 0, 0, 0, 0, 0 ], [ 0, 4, 0, 0, 0, 0, 0, 0, 0 ], [ 1, 3, 0, 0, 0, 0, 0, 0, 0 ], [ 0, 2, 1, 0, 0, 0, 0, 0, 1 ], [ 0, 3, 0, 1, 0, 0, 0, 0, 0 ], [ 0, 3, 0, 1, 0, 0, 0, 0, 0 ], [ 2, 1, 0, 0, 1, 0, 0, 0, 0 ], [ 0, 3, 0, 0, 0, 1, 0, 0, 0 ], [ 0, 3, 0, 0, 0, 0, 0, 1, 0 ] ] gap>
‣ AcceptedWords( aut, int ) | ( function ) |
Returns: All words of length int that are accepted by the automaton aut.
AcceptedWords outputs all permutations accepted by the automaton aut, which have length int, in a list. The permutations are output in their rank encoding.
gap> AcceptedWords(ba,1); [ [ 2 ], [ 3 ], [ 4 ] ] gap> AcceptedWords(ba,16); [ [ 4, 1, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 1, 1 ] ] gap>
‣ AcceptedWordsR( aut, int1[, int2] ) | ( function ) |
‣ AcceptedWordsReversed( aut, int1[, int2] ) | ( function ) |
Returns: The list of all by the automaton accepted words of length int1, where each word is written in reverse.
The functions AcceptedWordsR and AcceptedWordsReversed are synonymous and take the following arguments; an automaton aut, an integer int1 which indicates the length of the words that are accepted by the aut and another integer int2 which is optional and represents the initial state of aut. The return value of these functions is the list containing all permutations of length int1 that are accepted by aut. The permutations are rank encoded and written in reverse.
gap> AcceptedWordsR(ba,1); [ [ 2 ], [ 3 ], [ 4 ] ] gap> AcceptedWordsReversed(ba,16); [ [ 1, 1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 1, 4 ] ] gap>
generated by GAPDoc2HTML