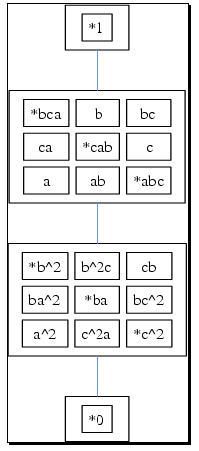
There are some pictures that may give a lot of information about a semigroup. This is the case of the egg-box picture of the D-classes, the right Cayley graph of a finite monoid and the Schützenberger graphs of a finite inverse monoid.
‣ DrawDClassOfElement( arg ) | ( function ) |
This function uses DotForDrawingDClassOfElement (3.1-2) to compute the dot code to produce the image that is then displayed. It takes as arguments a semigroup followed by a transformation which is the element whose D-class will be drawn. Optionally we can then specify n lists of elements and the elements of each list will be drawn in different colours. Finally, if the last argument is the integer 1 then the elements will appear as transformations, otherwise they will appear as words. The idempotents will be marked with a * before them.
This last optional argument may also be the integer 2 and in this case the elements will appear as integers, where i represents the element Elements(S)[i].
gap> DrawDClassOfElement(poi3, Transformation([1,4,3,4])); gap> DrawDClassOfElement(poi3, Transformation([1,4,3,4]),1); gap> DrawDClassOfElement(poi3, Transformation([1,4,3,4]), [Transformation( [ 2, 3, 4, 4 ] )],1); gap> DrawDClassOfElement(poi3, Transformation([1,4,3,4]), [Transformation( [ 2, 3, 4, 4 ] ), Transformation( [ 2, 4, 3, 4 ] )], [Transformation( [ 2, 4, 3, 4 ] )],1); gap> DrawDClassOfElement(poi3, Transformation([1,4,3,4]), [Transformation( [ 2, 4, 3, 4 ] )],"Dclass",1);
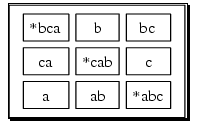
This is the image produced by the first command in the previous example:

‣ DotForDrawingDClassOfElement( arg ) | ( function ) |
This function computes the dot code that can be used to produce a drawing for the D-class of an element of a semigroup. This can be done by using the function DrawDClassOfElement (3.1-1) (if the system is properly configured) or by the user in some independent way. The arguments and options are the same than those of DrawDClassOfElement (3.1-1).
gap> DotForDrawingDClassOfElement(poi3,Transformation([1,4,3,4]));
"digraph DClassOfElement {\ngraph [center=yes,ordering=out];\nnode [shape=pla\
intext];\nedge [color=cornflowerblue,arrowhead=none];\n1 [label=<\n<TABLE BORD\
ER=\"0\" CELLBORDER=\"0\" CELLPADDING=\"0\" CELLSPACING=\"0\" PORT=\"1\">\n<TR\
><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR><TD BGCOLOR=\"white\" BORDER=\"\
0\">*abc</TD></TR>\n</TABLE></TD><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR\
><TD BGCOLOR=\"white\" BORDER=\"0\">a</TD></TR>\n</TABLE></TD><TD BORDER=\"0\"\
><TABLE CELLSPACING=\"0\"><TR><TD BGCOLOR=\"white\" BORDER=\"0\">ab</TD></TR>\
\n</TABLE></TD></TR>\n<TR><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR><TD BG\
COLOR=\"white\" BORDER=\"0\">bc</TD></TR>\n</TABLE></TD><TD BORDER=\"0\"><TABL\
E CELLSPACING=\"0\"><TR><TD BGCOLOR=\"white\" BORDER=\"0\">*bca</TD></TR>\n</T\
ABLE></TD><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR><TD BGCOLOR=\"white\" \
BORDER=\"0\">b</TD></TR>\n</TABLE></TD></TR>\n<TR><TD BORDER=\"0\"><TABLE CELL\
SPACING=\"0\"><TR><TD BGCOLOR=\"white\" BORDER=\"0\">c</TD></TR>\n</TABLE></TD\
><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR><TD BGCOLOR=\"white\" BORDER=\"\
0\">ca</TD></TR>\n</TABLE></TD><TD BORDER=\"0\"><TABLE CELLSPACING=\"0\"><TR><\
TD BGCOLOR=\"white\" BORDER=\"0\">*cab</TD></TR>\n</TABLE></TD></TR>\n</TABLE>\
>];\n}\n"
By using Print (or PrinTo, if one wants to print to a file) the string is displayed as follows:
gap> Print(last); digraph DClassOfElement { graph [center=yes,ordering=out]; node [shape=plaintext]; edge [color=cornflowerblue,arrowhead=none]; 1 [label=< <TABLE BORDER="0" CELLBORDER="0" CELLPADDING="0" CELLSPACING="0" PORT="1"> <TR><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BORDER="0">*\ abc</TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">a</TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">ab</TD></TR> </TABLE></TD></TR> <TR><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BORDER="0">b\ c</TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">*bca</TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">b</TD></TR> </TABLE></TD></TR> <TR><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BORDER="0">c\ </TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">ca</TD></TR> </TABLE></TD><TD BORDER="0"><TABLE CELLSPACING="0"><TR><TD BGCOLOR="white" BOR\ DER="0">*cab</TD></TR> </TABLE></TD></TR> </TABLE>>]; }
‣ DrawDClasses( arg ) | ( function ) |
This function is similar to the previous one, except that this one draws all the D-classes of the semigroup given as the first argument. It then takes optionally n lists of elements and the elements of each list will be drawn in different colours. It also accepts, as an optional argument, the integer 1, to specify whether the elements will appear as words or as transformations as in the previous function. The idempotents will be marked with a * before them.
The dot code is computed by DotForDrawingDClasses (3.2-2).
This last optional argument may also be the integer 2 and in this case the elements will appear as integers, where i represents the element Elements(S)[i].
gap> DrawDClasses(poi3); gap> DrawDClasses(poi3, [Transformation( [ 2, 3, 4, 4 ] ), Transformation( [ 2, 4, 3, 4 ] )], [Transformation( [ 2, 4, 3, 4 ] )],1);
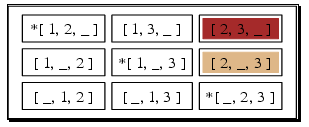
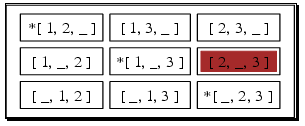
This is the image produced by the first command in the previous example:
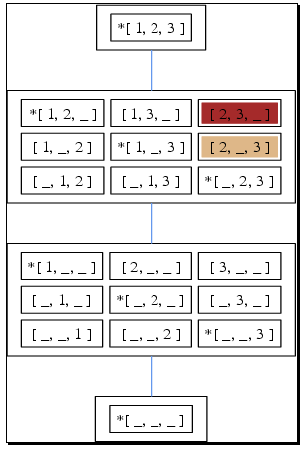
‣ DotForDrawingDClasses( arg ) | ( function ) |
This function computes the dot code that can be used to produce a drawing for the D-class of an element of a semigroup. This can be done by using the function DrawDClasses (3.2-1) (if the system is properly configured) or by the user in some independent way. The arguments and options are the same than those of DrawDClasses (3.2-1).
gap> Print(DotForDrawingDClasses(poi3)); digraph DClasses { graph [center=yes,ordering=out]; node [shape=plaintext]; edge [color=cornflowerblue,arrowhead=none]; ## ... many more lines ... </TABLE></TD></TR> </TABLE>>]; 4:4 -> 3:3; 3:3 -> 2:2; 2:2 -> 1:1; }
‣ DrawRightCayleyGraph( S ) | ( function ) |
Draws the right Cayley graph of a finite monoid or semigroup S.
‣ DrawCayleyGraph( S ) | ( function ) |
This function is a synonym of DrawRightCayleyGraph (3.3-1).
For example, the command DrawCayleyGraph(b21); would produce the following image (where state i represents the element Elements(S)[i], the neutral element is coloured in "light blue" and all other idempotents are coloured in "light coral"):
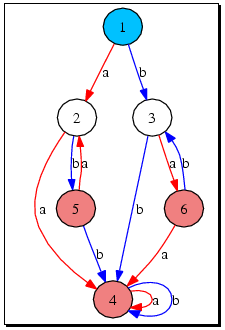
‣ DotForDrawingRightCayleyGraph( S ) | ( function ) |
This function computes the dot code that is used by the previous function and can also be used by the reader in some independent way.
‣ DrawSchutzenbergerGraphs( S ) | ( function ) |
Draws the Schützenberger graphs of the inverse semigroup S.
For example, DrawSchutzenbergerGraphs(poi3); would produce the following:
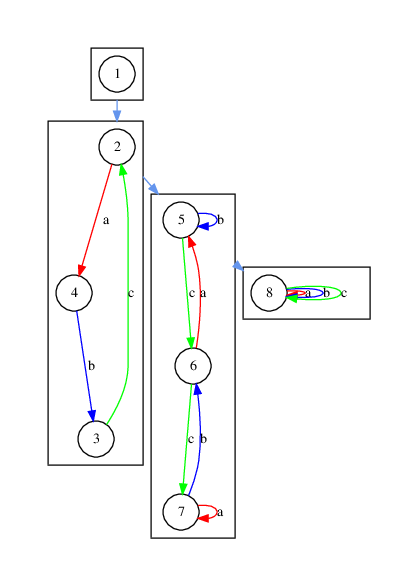
‣ DotForDrawingSchutzenbergerGraphs( arg ) | ( function ) |
This function computes the dot code that can be used to produce a drawing for the Schutzenberger Graphs of an inverse semigroup. This can be done by using the function DrawSchutzenbergerGraphs (3.4-1) (if the system is properly configured) or by the user in some independent way. The argument is an inverse semigroup.
gap> DotForDrawingSchutzenbergerGraphs(poi3); "digraph SchutzenbergerGraphs{\ncompound=true;\nsubgraph cluster4{\n1 [shape=\ circle];\n}\nsubgraph cluster3{\n2 -> 4 [label=\"a\",color=red];\n3 -> 2 [labe\ l=\"c\",color=green];\n4 -> 3 [label=\"b\",color=blue];\n2 [shape=circle];\n3 \ [shape=circle];\n4 [shape=circle];\n}\nsubgraph cluster2{\n5 -> 5 [label=\"b\"\ ,color=blue];\n5 -> 6 [label=\"c\",color=green];\n6 -> 5 [label=\"a\",color=re\ d];\n6 -> 7 [label=\"c\",color=green];\n7 -> 7 [label=\"a\",color=red];\n7 -> \ 6 [label=\"b\",color=blue];\n5 [shape=circle];\n6 [shape=circle];\n7 [shape=ci\ rcle];\n}\nsubgraph cluster1{\n8 -> 8 [label=\"a\",color=red];\n8 -> 8 [label=\ \"b\",color=blue];\n8 -> 8 [label=\"c\",color=green];\n8 [shape=circle];\n}\n1\ -> 2 [lhead=cluster3,ltail=cluster4,color=cornflowerblue];\n2 -> 5 [lhead=clu\ ster2,ltail=cluster3,color=cornflowerblue];\n5 -> 8 [lhead=cluster1,ltail=clus\ ter2,color=cornflowerblue];\n}\n"
By using Print (or PrinTo, if one wants to print to a file) the string is displayed as follows:
gap> Print(last); digraph SchutzenbergerGraphs{ compound=true; subgraph cluster4{ 1 [shape=circle]; } subgraph cluster3{ 2 -> 4 [label="a",color=red]; 3 -> 2 [label="c",color=green]; 4 -> 3 [label="b",color=blue]; 2 [shape=circle]; 3 [shape=circle]; 4 [shape=circle]; } subgraph cluster2{ 5 -> 5 [label="b",color=blue]; 5 -> 6 [label="c",color=green]; 6 -> 5 [label="a",color=red]; 6 -> 7 [label="c",color=green]; 7 -> 7 [label="a",color=red]; 7 -> 6 [label="b",color=blue]; 5 [shape=circle]; 6 [shape=circle]; 7 [shape=circle]; } subgraph cluster1{ 8 -> 8 [label="a",color=red]; 8 -> 8 [label="b",color=blue]; 8 -> 8 [label="c",color=green]; 8 [shape=circle]; } 1 -> 2 [lhead=cluster3,ltail=cluster4,color=cornflowerblue]; 2 -> 5 [lhead=cluster2,ltail=cluster3,color=cornflowerblue]; 5 -> 8 [lhead=cluster1,ltail=cluster2,color=cornflowerblue]; }
generated by GAPDoc2HTML