This chapter describes two Tcl/Tk graphical interfaces that can be used to define and edit semigroups and automata.
‣ XAutomaton( [A] ) | ( function ) |
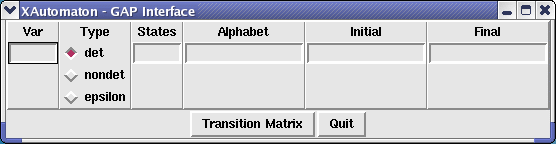
The function Xautomaton without arguments opens a new window where an automaton may be specified. A finite automaton (which may then be edited) may be given as argument.
gap> XAutomaton();
It opens a window like the following:

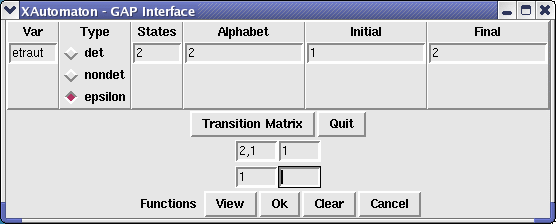
Var is the GAP name of the automaton, States is the number of states, Alphabet represents the alphabet and may be given through a positive integer (in this case the alphabet is understood to be a,b,c,... ) or through a string whose symbols, in order, being the letters of the alphabet. The numbers corresponding to the initial and accepting states are placed in the respective boxes. The automaton may be specified to be deterministic, non deterministic or with epsilon transitions. After pressing the transition matrix button the window gets larger and the transition matrix of the automaton may be given. The ith row of the matrix describes the action of the ith letter on the states. 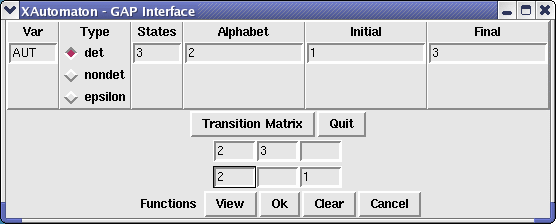
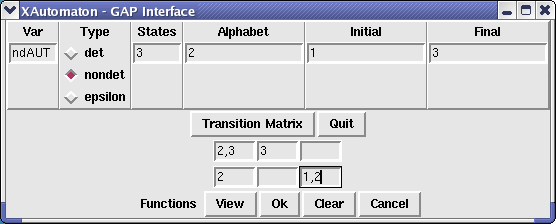
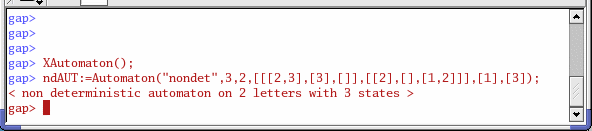
By pressing the button Ok the GAP shell aquires the aspect shown in the following picture and the automaton ndAUT may be used to do computations. Some computations such as getting a rational expression representing the language of the automaton, the (complete) minimal automaton representing the same language or the transition semigroup of the automaton, may be done directly after pressing the Functions button.
By pressing the button View an image representing the automaton is displayed in a new window.
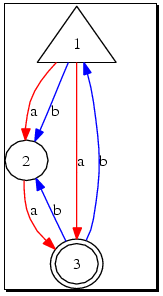
A new window with an image representing the automaton may be obtained by pressing the button View .
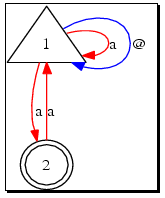
In the next example it is given an argument to the function XAutomaton.
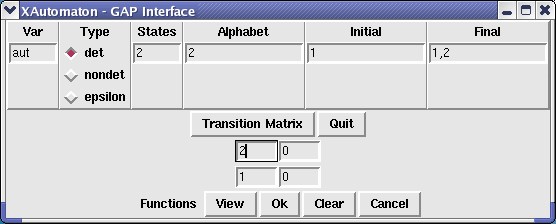
gap> A := RandomAutomaton("det",2,2); < deterministic automaton on 2 letters with 2 states > gap> XAutomaton(A);
It opens a window like the following:
The most common ways to give a semigroup to are through generators and relations, a set of (partial) transformations as generating set and as syntactic semigroups of automata or rational languages.
‣ XSemigroup( [S] ) | ( function ) |
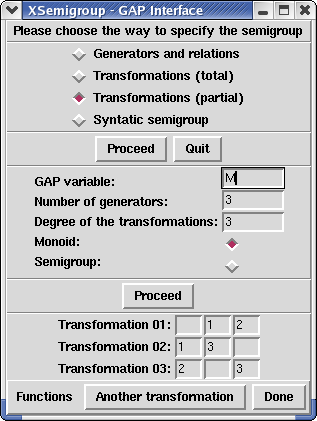
The function XSemigroup without arguments opens a new window where a semigroup (or monoid) may be specified. A finite semigroup (which may then be edited) may be given as argument.
gap> XSemigroup();
It opens a window like the following:

In the window opened by XSemigroup, by pressing the button Proceed the window should enlarge and have the following aspect. (If the window does not enlarge automatically, use the mouse to do it.)
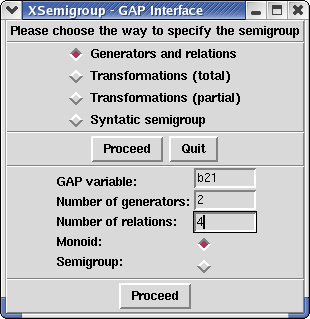
GAP variable is the GAP name of the semigroup. One has then to specify the number of generators, the number of relations (which does not to be exact) and whether one wants to produce a monoid or a semigroup. Pressing the Proceed button one gets: 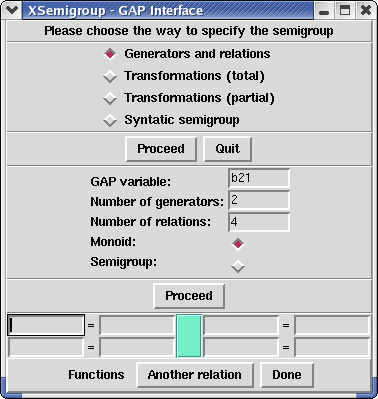
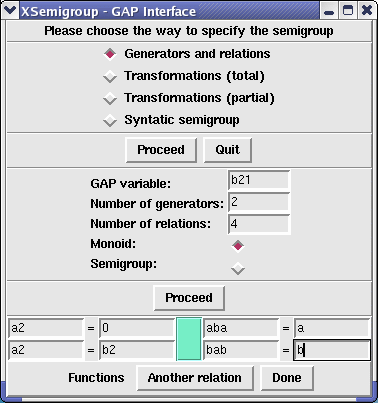
Pressing the Done button would output the following to the shell where GAP is running:

The menu button Functions has the following commands:
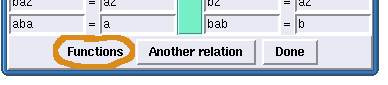

By pressing the menu button Functions and selecting "Draw Schutzenberger Graphs" would pop up the following window:
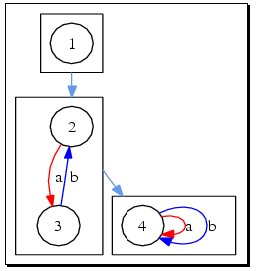
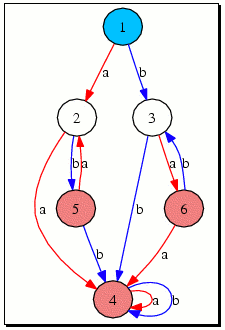
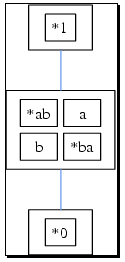
XSemigroup(poi3); would pop up the following window, where everything should be clear:
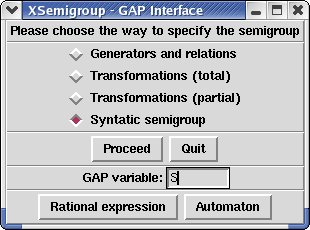
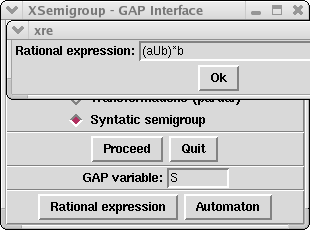
XSemigroup(); would pop up the following window, where we would select "Syntatic semigroup", press the Proceed button and then choose either to give a "Rational expression" or an "Automaton" by pressing one of those buttons:

generated by GAPDoc2HTML