Main Branches
Downloads Installation Overview Data Libraries Packages Documentation Contacts FAQ GAP 3Find us on GitHub
Navigation Tree
A p-Group with Special Properties
In the GAP Forum Reza Orfi asked:
Dear GAP Forum,
I need a p-Group G with these properties:
- Size(G) = p^n.
- Nilpotency Class of Group(G) = n-2.
- Center(G) is Cyclic Of Order p^2.
- DerivedSubgroup(G) = FrattiniSubgroup(G) .
- Size(DerivedSubgroup(G)) = p^(n-2).
One can easily verify that indeed there is no such group in the 'Small Groups Library', e.g. for order 256 running:
gap> g:= OneSmallGroup(256, FrattinifactorSize, 4, > g->Size(DerivedSubgroup(g)), 64, g->IsCyclic(Center(g)), true, > g->Size(Center(g)), 4); fail
In an answer to this Forum letter Bettina Eick showed that with the help of the package 'ANUPQ' the following functions can be used to answer the question:
gap> LoadPackage("anupq");
gap> CoclassPGroup := function( G ) > return Length(Factors(Size(G))) - Length(LowerCentralSeries(G))+1; > end;;
gap> TryPrime := function(p)
> local i, todo, news, H, desc, K;
> todo := [AbelianGroup([p,p])];
> i := 2;
> while true do
> i := i+1;
> Print("start layer ",i," with ",Length(todo)," groups \n");
> news := [];
> for H in todo do
>
> desc := PqDescendants( H : StepSize := 1 );
> Print( "Number of descendants: ", Length(desc), "\n");
> desc := Filtered(desc, x->Index(x,DerivedSubgroup(x))=p^2);
> for K in desc do
> if AbelianInvariants(Center(K)) = [p^2] then
> return K;
> fi;
> od;
> Append(news, Filtered( desc, IsCapable ));
> Print("\n");
>
> if CoclassPGroup(H) = 1 then
> desc := PqDescendants( H : StepSize := 2 );
> Print( "Number of descendants: ", Length(desc), "\n");
> desc := Filtered(desc,x->Index(x,DerivedSubgroup(x))=p^2);
> for K in desc do
> if AbelianInvariants(Center(K)) = [p^2] and
> CoclassPGroup(K) = 2 then
> return K;
> fi;
> od;
> Append(news, Filtered( desc, IsCapable ));
> Print("\n");
> fi;
> od;
> todo := StructuralCopy(news);
> if Length(todo) = 0 then return; fi;
> od;
> end;;
Since in the end we want to draw a lattice of certain subgroups, we have to do all calculations in XGAP.
We start this program for p = 3 and get (omitting some comments about the progress of the computation) a group of order 3^7:
gap> g:=TryPrime(3); <pc group of size 2187 with 7 generators>
To see a polycyclic presentation of this group we invoke the package 'Polycyclic' and use a print function from this:
gap> LoadPackage("polycyclic");
true
gap> gg:=PcGroupToPcpGroup(g);
Pcp-group with orders [ 3, 3, 3, 3, 3, 3, 3 ]
gap> PrintPcpPresentation(gg);
g1 ^ 3 = id
g2 ^ 3 = id
g3 ^ 3 = g6^2*g7^2
g4 ^ 3 = g7^2
g5 ^ 3 = g7
g6 ^ 3 = id
g7 ^ 3 = id
g2 ^ g1 = g2*g3
g3 ^ g1 = g3*g4
g3 ^ g2 = g3*g5
g4 ^ g1 = g4*g6
g4 ^ g2 = g4*g6
g4 ^ g3 = g4*g7^2
g5 ^ g1 = g5*g6*g7
g5 ^ g2 = g5*g6*g7^2
g5 ^ g3 = g5*g7^2
g6 ^ g1 = g6*g7
g6 ^ g2 = g6*g7^2
We verify:
gap> Size(Center(g)); 9 gap> IsCyclic(Center(g)); true gap> Collected(Factors(Size(DerivedSubgroup(g)))); [ [ 3, 5 ] ] gap> NilpotencyClassOfGroup(g); 5
We want to get some further idea of the structure of this group and determine information on its classes of elements and its subgroup lattice:
gap> C:=ConjugacyClasses(g);; gap> Length(C); 75 gap> Collected(List(C,x->[Order(Representative(x)),Size(g)/Size(Centralizer(x))])); [ [ [ 1, 1 ], 1 ], [ [ 3, 1 ], 2 ], [ [ 3, 3 ], 2 ], [ [ 3, 9 ], 2 ], [ [ 3, 81 ], 4 ], [ [ 9, 1 ], 6 ], [ [ 9, 3 ], 4 ], [ [ 9, 9 ], 4 ], [ [ 9, 27 ], 24 ], [ [ 9, 81 ], 8 ], [ [ 27, 27 ], 18 ] ] gap> LatticeSubgroups(g); <subgroup lattice of <pc group of size 2187 with 7 generators>, 88 classes, 926 subgroups> gap> S:=ConjugacyClassesSubgroups(g);; gap> Collected(List(S,x->[Size(Representative(x)),Size(g)/Size(Normalizer(g,Representative(x)))])); [ [ [ 1, 1 ], 1 ], [ [ 3, 1 ], 1 ], [ [ 3, 3 ], 1 ], [ [ 3, 9 ], 1 ], [ [ 3, 81 ], 2 ], [ [ 9, 1 ], 4 ], [ [ 9, 3 ], 3 ], [ [ 9, 9 ], 1 ], [ [ 9, 27 ], 10 ], [ [ 27, 1 ], 4 ], [ [ 27, 3 ], 3 ], [ [ 27, 9 ], 10 ], [ [ 27, 27 ], 7 ], [ [ 81, 1 ], 1 ], [ [ 81, 3 ], 13 ], [ [ 81, 9 ], 10 ], [ [ 243, 1 ], 1 ], [ [ 243, 3 ], 10 ], [ [ 729, 1 ], 4 ], [ [ 2187, 1 ], 1 ] ]We finally want to use XGAP to draw the lattice of normal subgroups of g and see the situation of the upper and lower central series of g. By
gap> s:= GraphicSubgroupLattice(g); <graphic subgroup lattice "GraphicSubgroupLattice">we open a window (to which we will refer as the 'XGAP window') just depicting the group g and its trivial subgroup. We now calculate the requested series in the GAP window and insert them into the drawing using a the menue 'subgroups' on the XGAP window.
We start (in the GAP window) by calculating the lower central series:
gap> LowerCentralSeries(g); [ <pc group of size 2187 with 7 generators>, Group([ f3, f4, f5, f6, f7 ]), Group([ f4, f5, f6, f7 ]), Group([ f6, f7 ]), Group([ f7 ]), Group([ <identity> of ... ]) ]
We now press the button 'Subgroups' in the XGAP window. This opens a menue, in which we press the button 'InsertVertices from GAP'. This causes the insertion of vertices for the groups of the lower central series into the XGAP window, while in the GAP window the process is reflected by:
gap> MenuSelected( 0, 2, 20 ); #I InsertVertices from GAP (G) --> (G,2,3,4,5,1)We now proceed analogously for the upper central series:
gap> UpperCentralSeries(g); [ Group([ f3, f4, f5, f6, f7, f1, f2 ]), Group([ f4, f5, f6, f7, f3 ]), Group([ f4*f5^2*f6, f6, f7, f5 ]), Group([ f4*f5^2*f6, f7, f6 ]), Group([ f4*f5^2*f6, f7 ]), Group([ ]) ] gap> MenuSelected( 0, 2, 20 ); #I InsertVertices from GAP (G) --> (G,2,3,6,7,1)
Finally we put the whole lattice of normal subgroups into the XGAP window pressing the button 'Normal Subgroups' in the menue 'Subgroups'. In the GAP window we see:
gap> MenuSelected( 0, 2, 17 ); #I Normal Subgroups (G) --> (G,8,9,10,11,2,3,12,13,6,14,15,16,7,4,5,1)
while in the XGAP window we see:
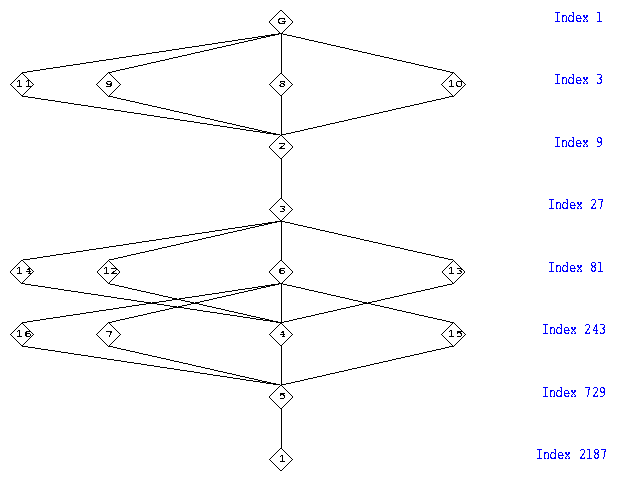
The lower central series in this picture is represented by (G > 2 > 3 > 4 > 5 > 1) while the upper central series is represented by (1 < 7 < 6 < 3 < 2 < G).
Finally we mention that the program of Bettina Eick does not produce a group with the requested properties for p = 2, even if run to high orders, thus indicating that probably there is no such 2-group, while e.g. for p = 5 it produces a group of order 5^9 with very similar structure as the 3-group that we have discussed here.